Preprints & Journal Articles
No. 14
Moritz Beyer, Stefano Mereta, Érika Roldán, Peter Voran
Higher-dimensional cubical sliding puzzles
We introduce higher-dimensional cubical sliding puzzles that are inspired by the classical 15 Puzzle from the 1880s. In our puzzles, on a d-dimensional cube, a labeled token can be slid from one vertex to another if it is topologically free to move on lower-dimensional faces. We analyze the solvability of these puzzles by studying how the puzzle graph changes with the number of labeled tokens vs empty vertices. We give characterizations of the different regimes ranging from being completely stuck (and thus all puzzles unsolvable) to having only one giant component where almost all puzzles can be solved. For the Cube, the Tesseract, and the Penteract (5-dimensional cube) we have implemented an algorithm to completely analyze their solvability and we provide specific puzzles for which we know the minimum number of moves needed to solve them.
Combinatorics; Algebraic Topology; and Discrete Configuration Spaces
Submitted, preprint arXiv:2307.14143
No. 13
Computational Complexity & Domination
Alexis Langlois-Rémillard, Mia Müssig, É. Roldán
Complexity of Chess Domination Problems
We study different domination problems of attacking and non-attacking rooks and queens on
polyominoes and polycubes of all dimensions. Our main result proves that the problem is NP-complete for non-attacking queens on polyominoes and for non-attacking rooks on three-dimen-sional polycubes. We also analyze these problems on the set of convex polyominoes, for which we conjecture and give some evidence that these domination problems restricted to this subset of polyominoes might be NP-completefor both, queens and rooks. We have also computed new values for classical queen domination problems on chessboards (square polyominoes). For our computations, we have translated the problem into an integer linear programming instance. Finally, using this computational implementation and the game engine Godot, we have developed a video game of minimal domination of queens and rooks on randomlygenerated polyominoes.
Submitted, preprint arXiv:2211.05651
No. 12

Extremal Combinatorics
É. Roldán, R. Toalá-Enríquez
Isoperimetric Formulas for Hyperbolic Animals
An animal is a planar shape formed by attaching congruent regular polygons along their edges. In 1976, Harary and Harborth gave closed isoperimetric formulas for Euclidean animals. Here, we provide analogous formulas for hyperbolic animals. We do this by proving a connection between Sturmian words and the parameters of a discrete analogue of balls in the graph determined by hyperbolic tessellations. This reveals a complexity in hyperbolic animals that is not present in Euclidean animals.
Submitted, preprint arXiv:2206.14910
No. 11

Combinatorics; Algebraic Topology
R. Karpman, É. Roldán
Parity Property of Hexagonal Sliding Puzzles
We study the puzzle graphs of hexagonal sliding puzzles of various shapes and with various numbers of holes. The puzzle graph is a combinatorial model which captures the solvability and the complexity of sequential mechanical puzzles. Questions relating to the puzzle graph have been previously studied and resolved for the 15 Puzzle which is the most famous, and unsolvable, square sliding puzzle of all time. It is known that for square puzzles such as the 15 Puzzle, solvability depends on a parity property that splits the puzzle graph into two components. In the case of hexagonal sliding puzzles, we get more interesting parity properties that depend on the shape of the boards and on the missing tiles or holes on the board. We show that for large-enough hexagonal, triangular, or parallelogram-shaped boards with hexagonal tiles, all puzzles with three or more holes are solvable. For puzzles with two or more holes, we give a solvability criterion involving both a parity property and the placement of tiles in tight corners of the board. The puzzle graph is a discrete model for the configuration space of hard tiles (hexagons or squares) moving on different tessellation-based domains. Understanding the combinatorics of the puzzle graph could lead to understanding some aspects of the topology of these configuration spaces.
Submitted
No. 10

Stochastic Topology &
First Passage Percolaion
F. Manin, É. Roldán, B. Schweinhart
Topology and local geometry of the Eden model
The Eden cell growth model is a simple discrete stochastic process which produces a "blob" in |R^d: start with one cube in the regular grid, and at each time step add a neighboring cube uniformly at random. This process has been used as a model for the growth of aggregations, tumors, and bacterial colonies and the healing of wounds, among other natural processes. Here, we study the topology and local geometry of the resulting structure, establishing asymptotic bounds for Betti numbers. Our main result is that the Betti numbers grow at a rate between the conjectured rate of growth of the site perimeter and the actual rate of growth of the site perimeter. We also present the results of computational experiments on finer aspects of the geometry and topology, such as persistent homology and the distribution of shapes of holes.
Discrete and Computational Geometry, February 2023
No. 09

Extremal Combinatorics
G. Malen, É. Roldán, R. Toalá-Enríquez
Extremal {p,q}-Animals
An animal is a planar shape formed by attaching congruent regular polygons, known as tiles, along their edges. In this paper, we study extremal animals defined on regular tessellations of the plane.
In 1976, Harary and Harborth studied animals in the Euclidean cases, finding extremal values for their vertices, edges, and tiles, when any one of these parameters is fixed. Here, we generalize their results to hyperbolic animals. We exhibit a sequence of spiral animals and prove that they attain the minimal numbers of edges and vertices within the class of animals with n tiles. In their conclusions, Harary and Harborth also proposed the question of enumerating extremal animals with a fixed number of tiles. This question has previously only been considered for Euclidean animals. We find special sequences of extremal animals that are unique extremal animals, in the sense that any animal with the same number of tiles which is distinct up to isometries can't be extremal.
Annals of Combinatorics, January 2023
No. 08

Extremal Topological Combinatorics
F. Manin, G. Malen, É. Roldán
High-dimensional Holeyominoes
What is the maximum number of holes enclosed by a d-dimensional polyomino built of n tiles? Represent this number by fd(n). Recent results show that f2(n)/n converges to 1/2. We prove that for all d≥2 we have fd(n)/n→(d−1)/d as n goes to infinity. We also construct polyominoes in d-dimensional tori with the maximal possible number of holes per tile. In our proofs, we use metaphors from error-correcting codes and dynamical systems.
Electronic Journal of Combinatorics, July 2022
No. 07
Stochastic Topology
M. Kahle, E. Paquette, É. Roldán
Topology of random 2-dimensional cubical complexes
We study a natural model of random 2-dimensional cubical com-plex which is a subcom-plex of an n-dimensional cube, and where every possible square 2-face is included independently with probability p. Our main result is to exhibit a sharp threshold p= 1/2 for homology vanishing as n→ ∞. This is a 2-dimensional analogue of the Burtin and Erdös–Spencer theorems characterizing the connectivity threshold for random cubical graphs. Our main result can also be seen as a cubical counterpart to the Linial–Meshulam theorem for random 2-dimensional simplicial complexes. However, the models exhibit strikingly different behaviors. We show that if p >1−√(1/2) ≈0.2929, then with high probability the fundamental group is a free group with one generator for every maximal 1-dimensional face.
Forum of Mathematics, Sigma, 29 November 2021.
No. 06
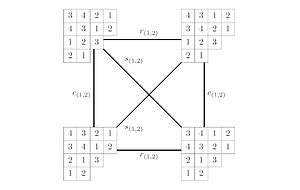
R. Karpman, É. Roldán
Isotopy Graphs of Latin Tableaux
Latin tableaux are a generalization of Latin squares, which first appeared in the early 2000s in a paper of Chow, Fan, Goemans, and Vondrák. Here, we extend the notion of isotopy, a per-mutation group action, from Latin squares to Latin tableaux. We define isotopy graphs for Latin tableaux, which encode the structure of orbits under the isotopy action, and investigate the relation-ship between the shape of a Latin tableau and the structure of its isotopy graph. Our main result shows that for any positive integer d, there is a Latin tableau whose isotopy graph is a d-dimensional cube. We show that most isotopy graphs are triangle-free, and we give a characterization of all the Latin tableaux for which the isotopy graph contains a triangle. We also give a formula for the degree of a vertex of each component of an isotopy graph which depends on both the shape of the Latin tableaux and the filling.
Discrete Configuration Spaces
Advances in Applied Mathematics, Volume 130, September 2021, 102204.
No. 05

H. Alpert, É. Roldán
Art Gallery Problem with Rook and Queen Vision
How many chess rooks or queens does it take to guard all squares of a given polyomino, the union of square tiles from a square grid? This question is a version of the art gallery problem in which the guards can ‘‘see’’ whichever squares the rook or queen attacks. We show that n/2 rooks or n/3 queens are sufficient and sometimes necessary to guard a polyomino with n tiles. We then prove that finding the minimum number of rooks or queens needed to guard a polyomino is NP-hard. These results also apply to d-dimensional rooks and queens on d-dimensional polycubes. Finally, we use bipartite matching theorems to describe sets of non-attacking rooks on polyominoes.
Computational Complexity & Domination
Graphs and Combinatorics 37(2), 621–642, Feb 2021
No. 04

G. Malen, É. Roldán
Polyiamonds Attaining Extremal Topological Properties, Part II
We consider two optimization questions with respect to polyiamonds. What is the maximum number of holes that a polyiamond with n tiles can enclose, and what is the minimum number of tiles required to construct a polyiamond with h holes? These numbers will be given by the sequences f△(n) and g△(h), respectively. In this paper, we construct a sequence of polyiamonds with hk= (3/2)(k^2−k) holes and nk= (1/2)(9k^2+3k−4) tiles such that g△(nk) =hk. Furthermore, these polyiamonds all attain a specific set of efficient geometric and topological properties.
Extremal Topological Combinatorics
Geombinatorics, Volume XXX, Issue 2, pages 63-76, Oct 2020
No. 03

G. Malen, É. Roldán
Polyiamonds Attaining Extremal Topological Properties, Part I
We consider two optimization questions with respect to polyiamonds. What is the maximum number of holes that a polyiamond with n tiles can enclose, and what is the minimum number of tiles required to construct a polyiamond with h holes? These numbers will be given by the sequences f△(n) and g△(h), respectively. In this paper, we construct a sequence of polyiamonds with hk= (3/2)(k^2−k) holes and nk= (1/2)(9k^2+3k−4) tiles such that g△(nk) =hk. Furthermore, these polyiamonds all attain a specific set of efficient geometric and topological properties.
Extremal Topological Combinatorics
Geombinatorics, Volume XXX, Issue 1, pages 14-24, July 2020
No. 02

Extremal Topological Combinatorics
G. Malen, É. Roldán
Extremal topological and geometric problems for polyominoes
We give a complete solution to the extremal topological combinatorial problem of finding the mini-mum number of tiles needed to construct a polyomino with h holes. We denote this number by g(h) and we analyze structural properties of polyominoes with h holes and g(h) tiles, characterizing their efficiency by a topological isoperimetric inequality that relates minimum perimeter, the area of the holes, and the structure of the dual graph of a polyomino. For h ≤ 8 the values of g(h) were originally computed by Tomas Olivera e Silva in 2015, and for the sequence hl=(2^(2l)−1)/3 by Kahle and Roldán in 2019, who also showed that asymptotically g(h)≈2h. Here we also prove that the polyominoes constructed by Kahle and Roldan with hl=(2^(2l)−1)/3 holes and g(hl) tiles are in fact unique up to isometry with these fixed parameters; that is, having the minimal number of tiles for hl holes.
Electronic Journal of Combinatorics, June 2020
No. 01

M. Kahle, É. Roldán
Polyominoes with maximally many holes
What is the maximum number of holes that a polyomino with n tiles can enclose? Call this number f(n). We show that if nk=(2^(2k+1)+3⋅2^(k+1)+4)/3 and hk=(2^(2k)−1)/3, then f(nk)=hk for k≥1. We also give nearly matching upper and lower bounds for large n, showing as a corollary that f(n)≈n/2.
Extremal Topological Combinatorics
Geombinatorics, Volume XXIX, Issue 1, pages 5-15, July 2019
Proceedings
No. 03

Educational Technology
E. Roldán, É. Roldán, D. K. Raave
Supporting education in marginalized communities with workshops combining music and mathematics
In this chapter, the authors present the experience of a series of workshops given in a marginalized community in Mexico during the COVID pandemic as a mean to mitigate the educational gap lockdowns provoked. The whole intervention consisted of 12 workshop sessions plus a closing activity. The workshops aimed to jointly promote learners' conceptual and procedural knowledge of basic mathematics and develop musical rhythmic awareness and sensitivity in a collaborative problem-solving manner. Seventy children, ranging from 8 to 12 years old, participated in the workshops facilitated by an educational game, namely Musical Monkeys, consisting of a board game and an app. Using an initial evaluation, the authors mapped students' profiles in terms of background knowledge (procedural and conceptual) to form balanced playing teams, including low and high achievers, and to adjust the workshops according to students' needs and levels. The setting, challenges encountered during the intervention, and future research directions are discussed.
Handbook of Integrating ICTs in STEAM Education, IGI Global, Chapter 15, pages 320-343, 2022.
No. 02

Educational Technology
E. Roldán, I. Chounta, É. Roldán
Learning music and math, together as one: Towards a collaborative approach for practicing math skills with music
In this paper we present a study that took place in an elementary school in Mexico. The study aimed to explore the use of a digital application for the design and orchestration of collabora-tive, game-based learning activities for STEAM and to study the impact of group formation with respect to students' background knowledge. The workshops took place in the form of a tournament where groups of students worked together to win sets of music and math rounds. The results indi-cate that homogeneous groups outperformed heterogeneous groups in terms of learning gains but heterogeneous groups achieved better results in terms of game score than homogeneous groups. The former does not confirm related research and it may suggest that the group formation impact on learning gains depends largely on the context. The latter may indicate the need for aligning the game objectives with learning goals in order to ensure that educational games indeed prioritize learning.
International Conference on Collaboration Technologies and Social Computing, Springer, pages 143-156, Sep 2020
No. 01

Combinatorics and Algorithms
Games & Puzzles
É. Roldán
The Mutando of Insanity
Puzzles based on coloured cubes and other coloured geometrical figures have a long history in the recreational mathematical literature. One of the most commercially famous of these puzzles is the Instant Insanity that consists of four cubes. Their faces are coloured with four different colours in such a way that each colour is present in each one of the four cubes. To solve the puzzle, one needs to stack the cubes in a tower in such a way that each one of the colours appears exactly once in the four long faces of the tower. The main purpose of this paper is to study the combinatorial richness of a mathematical model of this puzzle by analysing all possible ways of colouring the cubes to form a puzzle analogous to the Instant Insanity. We have done this analysis for n cubes and n colours for n=4,5,6. This combinatorial analysis allowed us to design the Mutando of Insanity, a puzzle that we presented at Gathering for Gardner 12 (G4G12).
G4G 12 Exchange Book, Proceedings of the 12 biennial conference Gathering for Gardner, 2017.
Software
No. 03

Combinatorics; Algebraic Topology
R. Karpman, É. Roldán
Discrete configurations spaces of sliding with hexagonal tiles
The code in this repository can be used to investigate the behavior of sliding puzzles on a subset of the tesselation of the plane by hexagons. For a board with squares tiles, is always possible to slide a square tile into a hole that shares an edge with the tile. For a board with hexagonal tiles, a tile can only slide into a neighboring empty hexagonal hole if there are two adjacent empty hexagons that are at the same time sharing an edge with the tile to move
The puzzle graph of a sliding puzzle is a graph whose vertices are configurations of the board. Two configurations are adjacent if one can be obtained from the other by sliding a tile into a hole. We are interested in characterizing the connected components of the puzzle graphs of puzzles with hexagonal tiles, which in turn allow us to determine whether a puzzle is solvable. We define functions that take a representation of a hexagonal board and a starting configuration as input and produce an output file containing a list of all configurations in the same connected component of the puzzle graph as the starting configuration.
GitHub; Lisence: GNU General Public License, Jan 2022
No. 02

A. Krymova, É. Roldán
Homology and Geometry of the Plaquette Eden Model
This package includes software to run simulations of the Plaquette Eden Model, which is a discrete 2-dimensional stochastic cell growth process defined on the 3-dimensional regular cubical tessellation of the Euclidian space. The software analyzes the topology (Betti numbers and persistent homology) and local geometry of the structure. The program also has visualization capabilities and can produce a picture of the Plaquette Eden Model or output a .txt file that can be used with Autodesk Maya to produce an interactive 3-dimensional image.
Ripser and GUDHI are used to compute and visulize persistent homology of the the Plaquette Eden Model. If you use this functionality, make sure to cite this library.
Stochastic Topology &
First Passage Percolation
GitHub; Lisence: GNU General Public License, May 2021
No. 01

A. Krymova, F. Manin, É. Roldán, B. Schweinhart
Topology and Geometry of the Eden Model
This package includes software to run simulations of the Eden Growth Model in Z^d in dimensions 2-5, and analyze the topology (Betti numbers and persistent homology) and local geometry of the structure. The software is also able to read a .txt file with the time at which tiles should be added. This allows analysis of simulations from other stochastic models. Note: the cells in a .txt file should be in chronological order. For graphical representation, the program can create a picture of a two-dimensional growth model and can output a .txt file for 3-dimensional growth modles which can be inputed to MAYA to produce an interactive 3-dimensional image.
GUDHI is used to compute homology and persistent homology in 3D, 4D, and 5D. If you use this functionality, make sure to cite this library.

